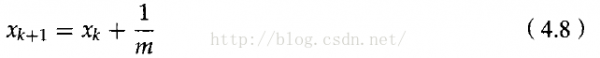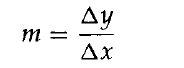计算机图形学(三)_图元的属性_10_ 通用扫描填充算法
来源:程序员人生 发布时间:2016-11-24 08:40:45 阅读次数:4103次
10 通用扫描填充算法
要实现区域的扫描线填充必须先肯定填充区边界与屏幕扫描线的交点位置。然后,将填充色利用于扫描线上位于填充区域内部的每段。扫描线填充算法利用奇偶规则辨认同1内部区域(参见)。最简单的填充区域是多边形,由于每扫描线和多边形的交点可通过求解1对联立的线性方程来取得,其中扫描线的方程是y
= 常数。
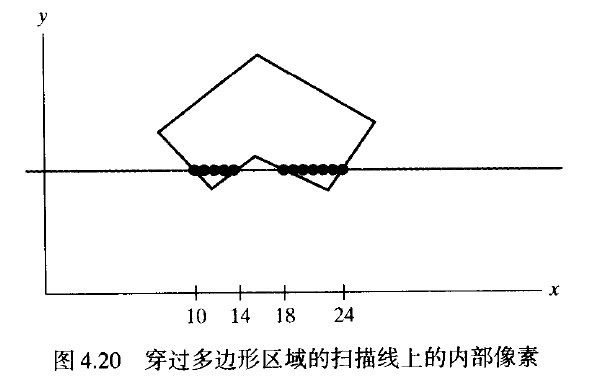
图4.20给出了多边形区域的实心填充的扫描线进程。对每条与多边形相交的扫描线,与边的交点从左向右排序,且将每对交点之间的像素位置包括这对交点在内,设定为指定色彩。在图4.20的例子中,与边界的4个交点像素位置定义了两组内部像素。这样,填充色利用于从x=10到x = 14的5个像素和从x
= 18到x = 24的7个像素。如果图案填充利用于多边形,则沿1条扫描线的每像素色彩由与填充图案堆叠的位置来肯定。
但是,多边形扫描线填充算法并
不如图4.20建议的那样简单。每当1条扫描线经过量边形的1个顶点时,扫描线在该顶点处与多边形的两条边相交。
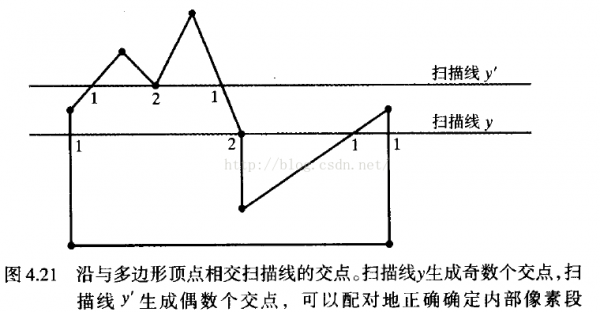
这类情况可能致使在这条扫描线的交点列表上要增加两个点。图4.21给出了在顶点处与多边形相交的两条扫描线。扫描线
y'与偶数条边相交,而在该扫描线上的两对交点正确地标识为内部像素段。但是扫描线
y与多边形的5条边相交。
要确认扫描线y的内部像素,必须将顶点处的交点看作为1个点。因此,在处理扫描线时,必须辨别这些情况。
通过关注相交边相对扫描线的位置,可以发现图4.21中扫描线
y和扫描线
y'间的
拓扑差异。
对扫描线y,同享1个顶点的两条相交边位于扫描线的
两侧。
但对扫描线y',两条相交边在扫描线的
同1侧。
因此,那些在扫描线两侧有连接边的顶点应当计为1个边界交点。可以通过顺时针或逆时针方向来搜索多边形边界,并视察
从1条边移到另外一条边时顶点y坐标的相对变化来辨认这个点。假设两条相邻边的3个端点
y'值
单调递增或递减,那末对任何穿过该顶点的扫描线,则
必须将该同享(中间)顶点计为1个交点。否则,同享的顶点表示多边形边界上的1个局部极值(最大或最小)。这两条边与穿过该顶点的扫描线的交点可以添加到相干列表中。
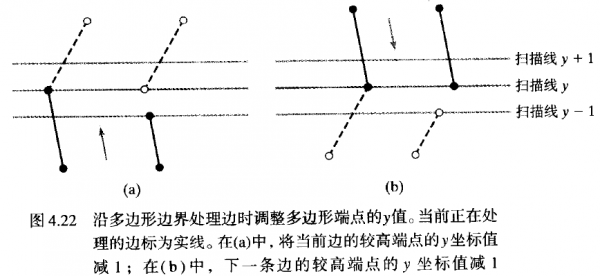
将顶点交点调剂为1个或两个的1种实现方法是将多边形的某些边缩短,从而分离那些应计为1个交点的顶点。我们可以依照指定的顺时针或逆时针方向处理全部多边形边界上的非水平边。在处理每条边时进行检测,肯定该边与下1条非水平边是不是有单调递增或单调递减的端点y值。假设有,可以将较低的1条边缩短,从而保证对通过公共顶点(连接两条边)的扫描线唯一1个交点生
成。图4.22给出了1条边的缩短情况。当两条边的端点y值递增时,将当前边的较高端点y值减去1,如图4.22(a)所示;当端点y值单调递减时,如图4.22(b)所示,就减去紧随当前边的1条边的较高端点y值。
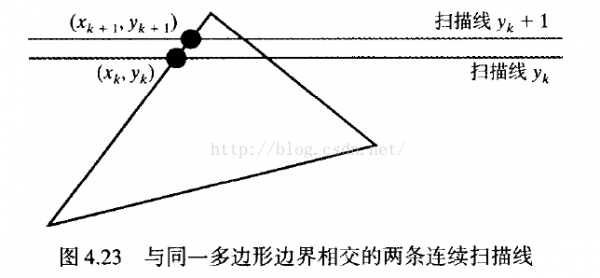
1般情况下,场景1部份的某些特点会以某种方式与该场景另外一部份的特点相干,且这些
相干特点(coherence property)可用于计算机图形算法中以减少处理。相干方法常常包括沿1条扫描线或在连续的扫描线间利用的增量计算。例如,在肯定填充区边的交点时,利用沿1条边从1条扫描线到下1条扫描时斜率为常数这1事实,可以沿任1边采取增量坐标计算。图4.23给出了与3角形左面1条边相交的两条连续扫描线,这条边的斜率可以用扫描线交点坐标来表示:
由于两条扫描线间y坐标的变化很简单:
上面1条扫描线的x交点值xk+ 1,可以通过前1条扫描线的x交点值xk戈来肯定:
因此,每一个后继交点的x值都可以通过增加斜率的倒数并取整而计算。
有关填充算法的最明显的并行实现方法,是将每条与多边形区域相交的扫描线分配给1个独立的处理器。然后分别完成每一个边交点的计算。扫描线k沿1条具有斜率m的边,相对最初扫描线的交点
xk值可计算为
在顺序填充算法中,沿1条边x方向的增量值l/m,可以通过调用斜率m为两整数比的整数运算来完成:
其中,△x和△y是该边端点x和Y坐标值之间的差。因此,沿1条边对连续两条扫描线交点的x增量计算可表示为
利用这个公式,可以完成交点x坐标的整数求值:先将计数器初始化为零,然后每当移向1条新的扫描线时,计数器就增加△x值,从而完成交点x坐标的整数求值。当计数器的值大于等于△y时,当前交点x值增加1,并将计数器减去△y。这个进程相当于保持交点x值的整数和小数部份,并增加小数部份直至到达下1个整数值。
作为整数增量的1个
例子,假定1条边的斜率为。m = 7/3。在起始扫描线处,我们将计数器设置为零,增量为3。当沿这条边移到其他3条扫描线时,计数器顺序地设置值3, 6和9。在初始扫描线以上的第3条扫描线上,计数器的值大于7。因此交点x坐标增加1,并重新将计数器设置为值9⑺=2。继续以这类方法肯定扫描线的交点值,直至到达边界的最高端点。对负斜率的边,可以通过一样的计算而得到交点。
我们可以不用舍人法以取得整数位置,而是取整到最接近的像素的x值,通过修改边的相交算法使得增量与△y/2相比较。在每步中计数器增加2△x值,并将增量与△y进行比较,当增量大于或等于△y值时,x值增加1,而计数器值减去2△y。在上面m = 7/3的例子中,对这条边上初始扫描线以上的几条扫描线,其计数器值变成6, 12(减少到⑵ ), 4, 10(减少到⑷ ) 2, 8(减少到⑹ ), 0, 6和12(减少到⑵)。在这条边的初始扫描线以上的第2, 4, 6, 9扫描线上.将增加x的值。每条边所需的额外计算是2△x
= △x + △x和2△y = △y + △y ,这些计算在预处理中完成。
为了有效地完成多边形填充,可以首先将多边形边界存储在
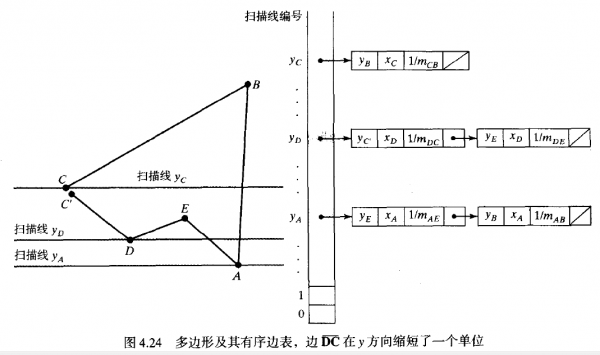
有序边表(sorted edge table)中,其中包括有效处理扫描线所需的全部信息。不管是以顺时针或逆时针沿边处理时,我们都可使用桶排序来存储各条边,按每条边的最小y值排序,存储在相应的扫描线位置。有序边表中仅存储非水平线。在处理边时,可以缩短某些边以解决顶点相交问题。对某条特定的扫描线,表中的每一个人口包括该边的最大y值、边的x交点值(在较低顶点处)和边斜率的倒数。对每条扫描线,以从左到右的顺序对边进行排序。图4.24给出了1个多边形及其相应的有序边表。
接下来,
从多边形的底部到顶部处理扫描线。对每条与多边形边界相交的扫描线生成1个活化边表(active edge list )。扫描线的活化边表包括所有与该扫描线相交的边,并使用重复相干性计算来得到边的交点。
边的相交计算也可通过将△x和△y值存储在有序边表中而得到简化。另外,为了确保对指定多边形内部的正确填充,可以利用在(像素编址和对象的几何要素)节中所讨论的斟酌情况。对每条扫描线,对从最左侧的x交点值到最右侧x交点值之间的每对x交点间的像素段进行填充。而每条多边形的边可以在顶部端点y方向上缩短1个单位,这类措施也能保证相邻多边形中的像素不会相互覆盖。
生活不易,码农辛苦
如果您觉得本网站对您的学习有所帮助,可以手机扫描二维码进行捐赠