Sparse Autoencoder稀疏自动编码

本系列文章都是关于UFLDL Tutorial的学习笔记

Neural Networks

• 对1个有监督的学习问题，训练样本输入情势为(x(i),y(i))。使用神经网络我们可以找到1个复杂的非线性的假定h(x(i))可以拟合我们的数据y(i)。我们先视察1个神经元的机制：

  

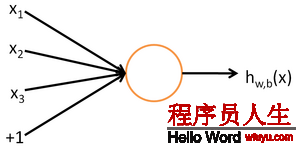
• 每一个神经元是1个计算单元，输入为x1,x2,x3，输出为：

  

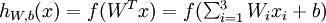
• 其中f()是激活函数，经常使用的激活函数是S函数：

  

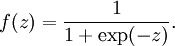
• S函数的形状以下，它有1个很好的性质就是导数很方便求：f’(z) = f(z)(1 − f(z))：

  

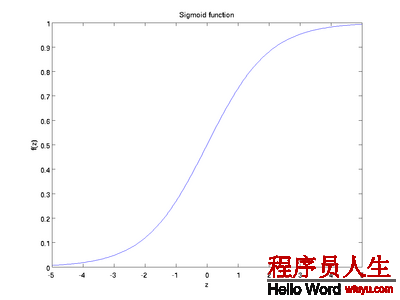
• 还有1个常见的激活函数是双曲正切函数tanh:

  

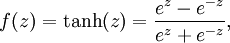
• 它的导数f’(z) = 1 − (f(z))^2):

  

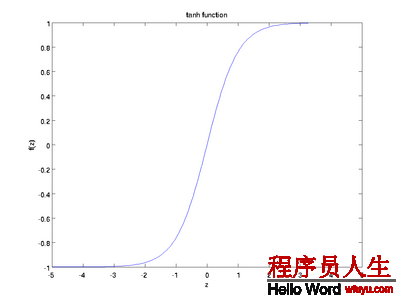
• softmax激活函数的导数：f’(z)=f(z)−f(z)^2

• S函数的取值在[0,1]之间，而tan函数的取值在[⑴,1]之间.

Neural Network model

• 神经网络就是将上面的单个神经元连接成1个复杂的网络：

  

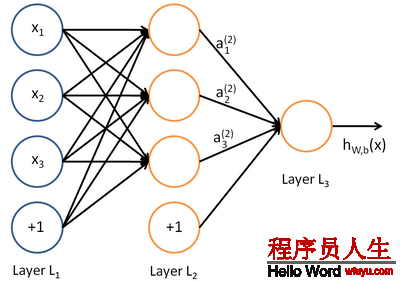
• 如图所示的3层神经网络包括1个输入层（3个输入单元），1个隐藏层（3个计算单元），1个输出层（1个输出单元）。我们的所有参数描写为(W,b) = (W(1),b(1),W(2),b(2))。Ws_ij表示的是第s层的第j个神经元到第s+1层的第i个神经元的权值，同理bs_i表示第s+1层的第i个神经元的偏差。可知，偏差b的数目等于总的神经元的个数减去输入层的神经元个数（输入层不需要偏差），而权值w的数目等于神经网络的连接数。最后的输出计算以下：

  

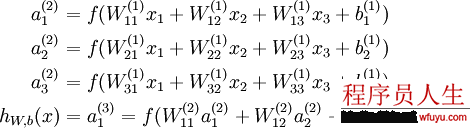
• 更紧凑的写法就是讲其写成向量的积，这样以矩阵的情势存储系数可以加速计算。其中z表示该层所有神经元的输入，a表示该层的输出：

  

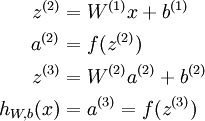
• 我们把上面这类求终究输出的算法称为向前传播（feedforward）算法。对输入层，我们可以用a1=x表示。给定l层的激活值al,计算l+1层的激活值的公式以下：

  

Backpropagation Algorithm

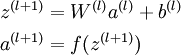
• 假定我们现在有1个固定大小为m的训练集{（x1,y1）,（x2,y2）…（xm,ym）}，我们使用批梯度降落法来训练我们的网络。对每一个训练样本（x,y），我们计算它的损失函数以下：

  

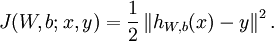
• 引入规范化（权重衰减项：weight decay），使得系数尽量的小，总的损失函数以下：

  

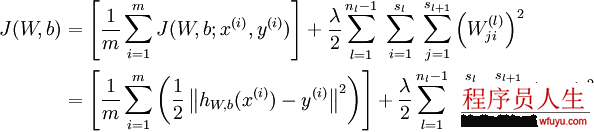
• 需要注意的是通常规范化不会使用在偏差b上，由于对b使用规范化终究取得网络和之前没有太大区分。这里的规范化实际上是贝叶斯规范化的1个变体，具体可以看CS229 (Machine Learning) at Stanford的视频。

• 上面的损失函数通常在分类和回归问题中被用到。在分类中通常y取值为0,1，而我们的S函数的取值范围是在[0,1]之间。而如果使用tanh函数，由于取值范围是[⑴,1]，我们可以将⑴表示0，1表示1，可以将0作为分界值。对回归问题我们则需要先将我们的输出按比例缩小到[0,1]之间，然后最后预测时相应的放大。

• 我们的目标是最小化损失函数J：首先随机初始化w和b，由于梯度降落法容易局部最优，因此要进行屡次实验，每次随机选择的参数不能相同。计算完所有样本的损失后，更新w和b的公式以下，其中α是学习率：

  

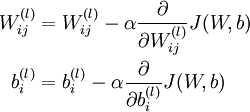
• 对这个更新公式，最核心的是计算偏导。我们采取反向传播（ backpropagation）算法来计算偏导。反向传播能够帮助解释网络的权重和偏置的改变是如何改变代价函数的。归根结柢，它的意思是指计算偏导数∂C/∂wl_jk和∂C/∂bl_j。但是为了计算这些偏导数，我们首先介绍1个中间量，δl_j，我们管它叫做第l层的第j个神经元的毛病量(error)。我们可以先计算1个样本产生的梯度向量，最后求所有样本梯度的平均便可：

  

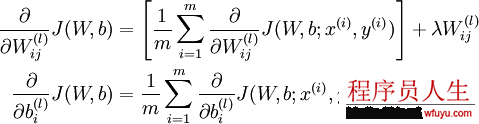
反向传播具体推导以下：

1. 首先使用向前传播计算出L2,L3…和输出层的激活值。

2. 对输出层的每个输出单元计算毛病量（a=f(z)利用偏导的链式法则）：

   

3. 对中间的隐藏层，我们计算每一个神经元的毛病量。其中括号里面可以理解为l+1层所有与l层该神经元相连的偏导乘以权值即为该神经元的损失值：

   

4. 定义偏导以下：

   

• 训练神经网络的伪代码以下（后面的λW是规范化项）：

根据neural networks and deep learning这本书中对反向传播是这么理解的：

• 对第l层第j个神经元，如果zl_j变成zl_j+Δzl_j，那末会对终究整体的损失带来(∂C/∂zl_j)*Δzl_j的改变。反向传播的目的是找到这个Δzl_j，使得终究的损失函数更小。假定∂C/∂zl_j的值很大（不论正负），我们期望找到1个和∂C/∂zl_j符号相反的Δzl_j使得损失下降。假定∂C/∂zl_j的值趋近于0，那末Δzl_j对损失的改变是微不足道的，表示这个神经元和训练接近最优了。这里以1个启发式的感觉将∂C/∂zl_j看成度量1个神经元的误差的方法。

• 受上面的启发，我们可以定义第l层第j个神经元的误差是：

  

• 输出层误差的方程，这个是根据偏导数链式法则 ∂C/∂z= （∂C/∂a）*（∂a/∂z） ：

  
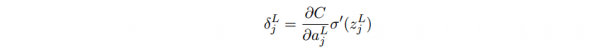
  右式第1项表示代价随着第j个神经元的输出值的变化而变化的速度。假设C不太依赖1个特定的神经元j，那末δl_j就会很小，这也是我们想要的效果。右式第2项刻画了在zl_j处激活函数σ变化的速度。如果使用2次代价函数，那末∂C/∂al_j = (aj − yj)很容易计算。

• 使用下1层的误差δl+1来表示当前层的误差δl，由于输出层是可以肯定的计算出来，因此计算其它层要倒着向前传播：

  其中 (wl+1)T是第l+1层权重矩阵 wl+1的转置。假定我们知道第l+1层的误差δl+1，当我们利用转置的权重矩阵(wl+1)T，我们可以凭直觉地把它看做是在沿着网络反向移动误差，给了我们度量在第l层输出的误差方法，我们进行Hadamard（向量对应位置相乘）乘积运算 ⊙σ′(zl)。这会让误差通过 l 层的激活函数反向传递回来并给出在第 l 层的带权输入的误差 δ向量。

• 代价函数关于网络中任意偏置的改变率：

  误差 δl_j 和偏导数值∂C/∂bl_j 完全1致，针对同1个神经元。

• 代价函数关于任何1个权重的改变率：

  
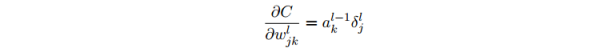
  这告知我们如何计算偏导数∂C/∂wl_jk，其中 δl 和 al−1 这些量我们都已知道如何计算了。

• 将其向量化：

  其中 ain是输入给权重 w 的神经元的激活值， δout 是输出自权重 w 的神经元的误差。当激活值 ain 很小， ain ≈ 0，梯度∂C/∂w 也会趋向很小。这样，我们就说权重缓慢学习，表示在梯度降落的时候，这个权重不会改变太多。换言之， 来自低激活值神经元的权重学习会非常缓慢。

• 当 σ(zl_j) 近似为 0 或 1 的时候 σ 函数变得非常平。这时候σ’(zl_j) ≈ 0。所以如果输出神经元处于或低激活值（ ≈ 0）或高激活值（ ≈1）时，终究层的权重学习缓慢。这样的情形，我们常常称输出神经元已饱和了，并且，权重学习也会终止（或学习非常缓慢）。如果输入神经元激活值很低，或输出神经元已饱和了（太高或太低的激活值），权重会学习缓慢。

• 第2个方程的证明

• 反向传播进程给出了1种计算代价函数梯度的方法：

• 给定1个大小为 m 的小批量数据，在这个小批量数据的基础上利用1步梯度降落学习算法：

• 对l层的第j个神经元的权值做1点修改，会致使1些列激活值的变化：

• ∆wl_jk 致使了在第l层 第j个神经元的激活值的变化 ∆al_j。

• ∆al_j 的变化将会致使下1层所有激活值的变化，我们聚焦到其中1个激活值上看 看影响的情况，无妨设 al+1_q :

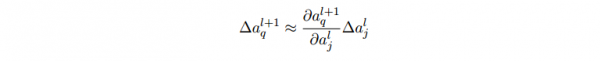
• 这个变化 ∆al+1_q 又会去下1层的激活值。实际上，我们可以想象出1条从 wl_jk到 C 的路径，然后每一个激活值的变化会致使下1层的激活值的变化，终究是输出层的代价的变化。假定激活值的序列以下 al_j, al+1_q, …,
  aL⑴_n, aL_m，那末结果的表达式就是:

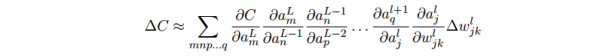
• 我们用这个公式计算 C 关于网络中1个权重的变化率。这个公式告知我们的是：两个神经元之间的连接实际上是关联于1个变化率因子，这个因子是1个神经元的激活值相对其他神经元的激活值的偏导数。从第1个权重到第1个神经元的变化率因子是 ∂al_j/∂wl_jk。路径的变化率因子其实就是这条路径上的众多因子的乘积。而全部的变化率 ∂C/∂wjk l就是对所有可能的从初始权重到终究输出的代价函数的路径的变化率因子的和。针对某1个路径，这个进程解释以下：

Gradient checking and advanced optimization

• 在本节中，我们描写了1个数值方法用来检查你求解导数的代码是不是正确，进行导数检查进程将大大增加你的代码的正确性。

• 假定我们想最小化J(θ)，我们可以进行梯度降落：
  

• 假定我们找到1个函数g(θ)等于这个导数，那末我们如何确认这个g(θ)是不是正确呢？回想导数的定义：
  

• 我们可以比较上式和g(θ)是不是1样来检验函数g是不是正确，通常ε设置为1个很小的数（比如10^⑷）。假定ε=10^⑷，通常你会发现上面两个式子最少有4位有效数字是1样的（通常会更多）

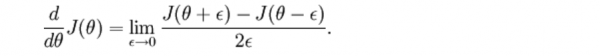
• 现在斟酌θ是个向量而不是1个值，我们定义：
  

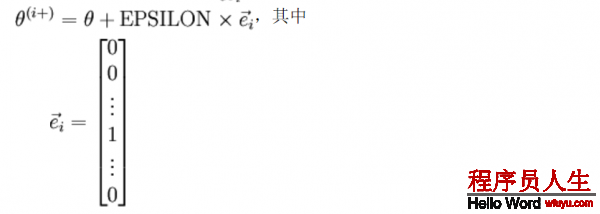
• 其中θi+和θ几近相同，除第i个位置上增加ε。

• 我们可以对每一个i 检查下式是不是成立，进而验证gi(θ)的正确性：
  

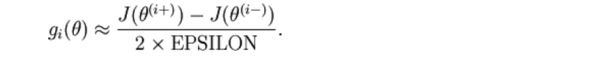
• 再利用反向传播求解神经网络时，正确的算法会得到下面这样的导数，我们需要使用上面的方法来验证得到的导数是都正确：